PERCEVOIR LES CONCEPTS GEOMETRIQUES aux cycles 2 et 3
Année scolaire
2022 / 2023
Problématique
Comment mettre en place des automatismes en géométrie par l’utilisation de rituels ?
Groupe d’enseignants
Ecoles d’Avressieux – Belmont-Tramonet – Champagneux
Classes à double ou triple niveaux cycle 2 / cycle 3
Formateur
sandrine.poinas [at] ac-grenoble.fr (Sandrine Poinas)
Type de support
Le premier constat de départ des enseignantes de la constellation était que la géométrie est la plupart du temps le parent pauvre des fichiers et manuels. Il n’est pas facile de l’enseigner de manière satisfaisante à une classe entière car on aurait envie d’être derrière chaque élève lorsqu’il trace des figures. Et c’est encore plus complexe dans une classe à double ou triple niveaux.
Le second constat de départ est que pour les élèves soient capables de réaliser des figures précises en cycle 3, il faut qu’ils acquièrent d’abord les concepts sous-jacents et tout un vocabulaire spécifique à la géométrie.
L’hypothèse de la constellation est la suivante : s’appuyer sur des rituels et des activités travaillant davantage les concepts et le vocabulaire que la précisions des tracés, permettra de poser les bases nécessaires de la géométrie au cycle 3 et 4.
Ressources utilisées lors de la formation et productions de la constellation.
Les apports de Thierry Dias, didacticien, chercheur et professeur HEP Lausanne
La réflexion de la constellation s’est appuyée au départ sur les travaux de Thierry Dias, didacticien, chercheur et professeur à l’HEP de Lausanne. Il met en valeur l’importance de proposer de nombreuses expériences sensorimotrices avant de commencer à tracer des triangles ou des perpendiculaires. Il insiste également sur la nécessité de proposer aux élèves des problèmes à résoudre pour donner du sens à la géométrie.
Les deux documents ci-dessous présentent une synthèse de ces propos.
Expérimenter et vivre la géométrie
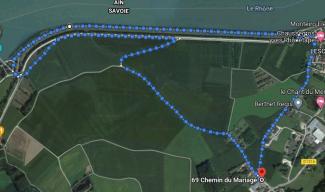
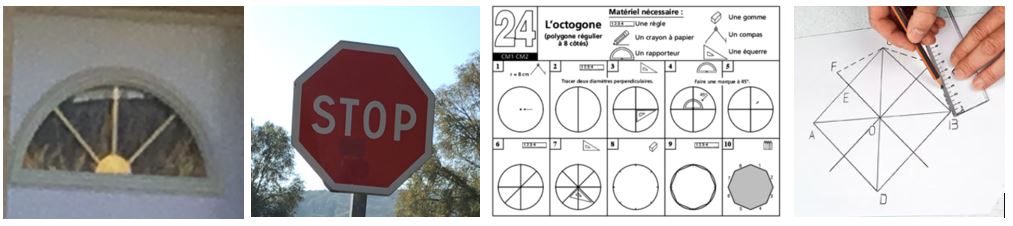
Activité 1 : La balade géométrique : À partir de quelques photographies, on peut imaginer différentes pistes d’exploitation pédagogique : une chasse aux formes géométriques, un jeu du “qui est-ce ?”, une description écrite à compléter, une représentation avec figures à main levée, un programme de construction à écrire.
Des ressources sur : https://www.mathsenvie.fr/
Témoignage de Romance C, enseignante en CM1-CM2 à Champagneux.
Avec ma classe, je sors régulièrement pour faire des promenades pédagogiques. Ces promenades sont fréquentes en pédagogie Freinet. M Freinet partait du principe qu’il fallait vivre les apprentissages pour les comprendre et les maitriser.
Ces promenades ont des objectifs différents comme « dessiner ce qu’on voit », « chercher des éléments mathématiques », « apprendre la géographie de notre territoire », « analyser des paysages ». etc.
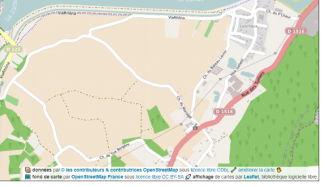
Lors des promenades mathématiques, les élèves chaussent leurs « lunettes mathématiques » (comme dirait Daniel Gostain) pour ne filtrer que la géométrie, ou les nombres… Nous commençons toujours par nous projeter dans le trajet (carte, google maps/openstreetmap). Nous voyons le parcours, la distance, les éléments que nous pourrions rencontrer.
Ensuite, nous récoltons des photos des éléments, nous nous arrêtons pour commenter les trouvailles et mettre le bon vocabulaire derrière chaque chose.
En classe, nous trions toutes les photos, nous élaborons un résumé collectif.
Ensuite, j’isole certains éléments pour travailler plus précisément dessus. Par exemple, comment tracer ces figures géométriques ?
Ou encore, nommer des solides, les caractériser : Une grande quantité de matériaux est récoltée pour amorcer des points du programme en classe. C’est très riche et tellement amusant ! On fait du sport, des sciences, de la géographie, du dessin ou des maths !
Activité 2 : La corde à 13 noeuds : Une activité pour travailler, à l’aide d’une corde à noeuds, la notion de polygone (figure fermée, côtés droits ou courbe) , de sommets, de parallèles, de perpendiculaires., réaliser des quadrilatères avec des angles droits.
Une séquence complète pour le cycle 2 et le cycle 3 sur : Géométrie avec la corde à 13 nœuds IREM de Montpellier.
Témoignage de Béatrice J, enseignante en CP-CE1 à Belmont-Tramonet
L'activité démarre par 3 grandes séances visant à découvrir la corde à 13 nœuds, à la présenter, à en définir les règles d'utilisation et à la manipuler en réalisant diverses figures géométriques.
Elle se prolonge par un rituel court de quelques minutes en début de chaque séance de math pendant plusieurs semaines reprenant les activités des 2ème et 3ème séances .
Activité 3 : Vivre l’alignement : Une activité, à réaliser au stade ou dans la cour de l’école, qui permet de comprendre la notion d’alignement
Proposée par : https://www.apmep.fr/Donner-vie-a-la-geometrie-au-cycle
Intégrer les concepts géométriques
Activité 1 : La géométrie mentale : Une activité pour aider les élèves à se forger une image mentale des objets ou des configurations géométriques planes ou de l’espace. (le document eduscol pour le cycle 3)
Témoignage de Christelle R, enseignante en CE1-CE2 à Champagneux.
J’ai suivi la programmation de géométrie mentale au cycle 2 proposée par Sylvie Attali.
Ces petits exercices ritualisés ont permis à mes élèves d’acquérir beaucoup de vocabulaire. Du plus simple (vertical/horizontal) au plus technique (noms des figures géométriques et propriétés).
En ce qui concerne les mots « horizontal » et « vertical » (qui ne sont finalement pas si simples), j’ai proposé des petites dictées très rapides. Au départ c’est moi qui dictais puis ce sont les enfants qui sont venus au tableau. Donc au tableau, un enfant dicte « Horizontal/vertical/vertical/horizontal ….. » et ses camarades, sur leur ardoise, font des traits dans le sens demandé. L’élève qui est au tableau a lui aussi fait les traits, pour corriger, il retourne le tableau. Très vite, les enfants ont ajouté d’autres mots de vocabulaire comme « ligne brisée ouverte », « ligne courbe fermée » ….
Tous ces exercices se font à main levée. Au départ, j’étais réticente et finalement je me suis rendue compte que ce travail était bénéfique. D’abord parce qu’il se fait vite et permet de faire beaucoup d’exercices et puis il est important pour ancrer les concepts et le vocabulaire. La précision des tracés viendra après.
Témoignage d’Anaëlle D, enseignante en CP-CE1 à Champagneux.
Le déroulement de cette activité de géométrie mentale est le suivant :
les enfants sortent leur ardoise et posent leur crayon pour être prêts à écouter
l’enseignant donne la consigne (ou la succession de consignes selon le niveau) et les élèves écoutent (ils ne tracent pas en même temps)
les élèves tracent à main levée sur leurs ardoises l’ensemble des consignes données en se souvenant des différentes formulations et précisions sur les dispositions des éléments
l’enseignant circule parmi eux et sélectionne quelques productions qui lui semblent intéressantes
mise en commun : l’enseignant montre à la classe les productions choisies (une à une) et l’ensemble de la classe valide ou non la production en justifiant à partir des consignes et en s’appuyant sur le vocabulaire géométriques et les caractéristiques connues (ex : il y a bien trois côtés à sa figures qui est fermée donc c’est bien un triangle). L’enseignant en profite pour expliquer aux élèves les notations géométriques, pour vérifier que le vocabulaire est bien utilisé et pour faire redéfinir aux élèves les caractéristiques des notions travaillées
En prolongement de ce rituel, on peut proposer à la classe le déroulé suivant :
faire venir un élève au tableau et dessiner sur son ardoise une situation proche de celles travaillées avec le rituel géométrique (qui refait travailler le vocabulaire étudiés et qui fait écho à des situations déjà rencontrées lors du rituel)
l’élève prend l’ardoise qu’il ne montre pas au reste de la classe et doit donner oralement les consignes aux autres élèves pour que chacun puisse être en mesure de tracer cette figure sur son ardoise (les consignes données doivent donc être précises et reprendre le vocabulaire géométrique)
l’élève circule ensuite pour valider ou non les productions, il peut ainsi se rendre compte des manques éventuels ou imprécisions de sa consigne
une mise en commun peut être faite ensuite pour trouver la formulation la plus simple afin de reproduire facilement et fidèlement la consigne
Après avoir testé quotidiennement ce rituel avec ma classe de CE1-CE2, j’ai constaté de rapides progrès par rapport à la maitrise du vocabulaire géométrique. Les élèves ont également beaucoup progressé sur leurs tracés et comprennent mieux les codages.
Témoignage de Romance C, enseignante en CM1-CM2 à Champagneux.
Voici une progression en géométrie mentale mise en œuvre dans ma classe cette année.

Activité 2 : La copie flash: L’enseignant montre la figure puis cache la figure. Les élèves doivent l’imaginer dans leur tête. Les élèves dessinent alors la figure à main levée sur l’ardoise. On vérifie en comparant au modèle.
Explications sur : https://ww2.ac-poitiers.fr/dsden16-pedagogie/sites/dsden16-pedagogie/IMG/pdf/projet__geometrie_copie_flash_geometrique.pdf
Activité 3 : Le jeu du portrait : a venir
Activité 4 : La dictée géométrique : Les élèves sont en possession d’une même figure complexe. L’enseignant fait comme s’il ne connaissait pas la figure, et réalise la figure, sous la dictée des élèves
Résoudre des problèmes géométriques
La restauration de figure : Une activité qui se base sur le fait de devoir compléter une figure cachée ou en partie effacée. Elle permet de travailler sur les propriétés géométriques des figures et d’aborder différents niveaux de visions (lignes, surfaces, ou points). Une présentation de la démarche, des activités préalables utilisables en rituels , ou avec des plus jeunes, une séquence de 4 séances pour construire et institutionnaliser, des activités de réinvestissement, une progression sur https://lea-geometrie.etab.ac-lille.fr/
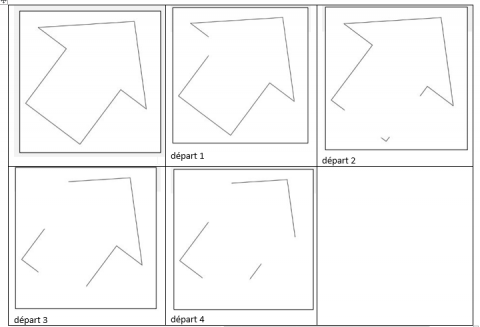
Témoignage de Romance C, enseignante en CM1-CM2 à Champagneux.
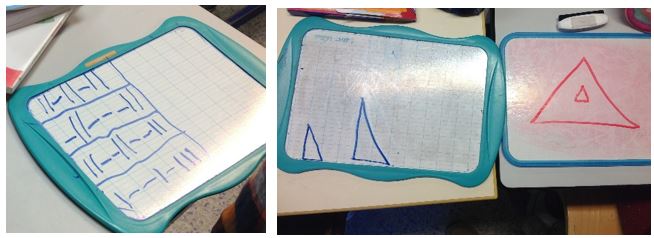
J’ai choisi d’aborder la restauration de figure en débutant par des figures à première vue très simples. J’ai, en effet, dans ma classe quelques élèves qui « ne voient pas dans l’espace », aussi, l’idée était de les familiariser avec le principe de reconstitutions simples avant de passer à des figures plus complexes.
Nous avons beaucoup verbalisé et j’ai demandé aux élèves les plus en difficulté de venir au tableau repasser avec leur doigt sur les côtés des figures (1,2,3). Ainsi, corporellement, ils sont arrivés à se représenter les figures complètes. Une fois à leur place, ils ont fait les mêmes tracés avec leur doigt avant de prendre leur matériel de géométrie. Ce travail est évidemment fait très vite par les élèves qui n’ont aucun problème avec la représentation sur différents plans.
Mes modèles de figures et de progression sont pris dans les documents suivants :
https://publimath.univ-irem.fr/numerisation/WO/IWO09008/IWO09008.pdf
https://www.apmep.fr/IMG/pdf/Perrin_Glorian_2.pdf
L’étape suivante était de partir d’un même modèle mais de le reconstituer à partir d’amorces différentes. L’objectif était d’obliger les élèves à voir la figure modèle sous des angles différents. A chaque fois, l’effort était porté sur la verbalisation du vocabulaire et de la méthode de reconstitution (prolonger, segment, sommet, angles, côté…). Les plus en difficulté devaient d’abord tracer avec leur doigt des figures simples reconnues (triangle, carré, rectangle) afin de se projeter plus efficacement dans la reconstitution.
Enfin, pour les dernières étapes de la progression, les reconstitutions à effectuer étaient volontairement orientées dans un autre sens que le modèle, pour inciter les élèves à tourner leur feuille de travail et observer les figures sous des angles différents.
Une progression intéressante : Géométrie : la restauration de figure une progression cycle 3
Travail élaboré lors du plan mathématique 2021-2022 - Constellation inter-degré - circonscription Arcachon sud – secteur du Val de l’Eyre :